| Chapter 2.6: Orbitals,
electron clouds, probabilities, and energies |
Our current working model of the atom is based on quantum mechanics – which incorporates the idea of quantized energy levels, the wave properties of electrons, and the uncertainties associated with electron location and momentum. If we know their energies, which we do, then the best we can do is to calculate a probability distribution that describes the likelihood of where a specific electron might be found (if we were to look for it, of course). If we were to find it, we would know next to nothing about its energy, which implies we would not know where it would be in the next moment. We refer to these probability distributions by the anachronistic, misleading, and Bohrian term “orbitals”. Why misleading? Because (to a normal person) the term orbital implies that the electron actually has a defined and observable orbit, something that is simply impossible to know (can you explain why?) |
2.1 Electrons & Orbitals |
Another common and often useful way to describe where the electron is in an atom is to talk about the electron probability density, or electron density for short. In this terminology, electron density represents the probability of an electron being within a particular volume of space; the higher the probability, the more likely it is in a particular region at a particular moment. Of course, you can't really tell if the electron is in that region at any particular moment, because if you did you would have no idea of where the electron would be in the next moment. A mathematical description of the behavior of electrons in atoms was developed by Erwin Schrödinger (1887–1961), and extended by Max Born (1882–1970). Schrödinger used the idea of electrons as waves and described each atom in an element by a mathematical wave function using the famous Schrödinger equation (HΨ = EΨ) – we assume that you have absolutely no idea what either HΨ or EΨ are, but not to worry, you don’t really need to. The solutions to the Schrödinger equation are a set of equations (wave functions) that describe the energies and probabilities of finding electrons in a region of space. They can be described in terms of a set of “quantum numbers” (recall that Bohr’s model also invoked the idea of quantum numbers). One way to think about this is that almost every aspect of an electron (within an atom or a molecule) is quantized – that is, only defined values are allowed for its energy, probability distribution, orientation, and “spin”. It is far beyond the scope of this book to present the mathematical and physical basis for these calculations, so we won’t pretend to try. However we can use the results of these calculations to provide a model for the arrangements of electrons in an atom - that is we can introduce the idea of orbitals - which are mathematical descriptions of the probability of finding electrons in space, and determining their energies. Let us take a look at some orbitals, their quantum numbers, energies, shapes and how they can be used to explain atomic behavior. Examining atomic structure using light: on the road to quantum numbers: All atoms are by definition electrically neutral - they contain equal numbers of positive and negatively charged particles, protons and electrons. We cannot remove a proton from an atom without changing the identity of the element, since the number of protons is how we define elements, but it is possible to add or remove an electron, leaving the atom’s nucleus unchanged. When an electron is removed or added to an atom it results in the atom having a net charge - atoms (or molecules) with a net charge are known as ions; and this process (atom/molecule to ion) is called ionization. A positively charged ion (called a cation) results when we remove an electron, a negatively charged ion (called an anion) results when we add an electron. Remember this added or removed electron becomes part of, or is removed from, the atom’s electron cloud. What we discover is that it takes 1312 kJ to remove a mole of electrons from a mole of hydrogen atoms. As we move to the next element, helium (He) – which has two electrons we find that the energy required to remove an electron from helium is 2373 kJ/mol - almost twice that required to remove an electron from hydrogen! Let us return to our model of the atom. Each electron in an atom is attracted by all the protons, located in essentially the same place (the nucleus), and at the same time the electrons repel each other. Coulomb’s law (?) tells us that the potential energy of the system is proportional to the product of the charges divided by the square of the distance between them. Therefore the energy to remove an electron from an atom should depend on the net positive charge acting upon the electron and the electron’s average distance from the nucleus. Since it is more difficult to remove an electron from a He atom than from an H atom, our tentative conclusion is that the electrons in helium must be attracted more strongly to the nucleus. In fact this makes sense: the He nucleus contains two protons, and each electron is attracted by both protons - making them more difficult to remove. They are not attracted exactly twice as strongly, since there are also some repulsive forces between the two electrons. |
| Based on the observation that i) helium has a higher ionization energy than hydrogen and ii) that helium atoms are smaller than hydrogen atoms, we infer that the electrons in helium are attracted more strongly to the nucleus than is the electron in hydrogen. Let us see if this trend continues as we move to the next heaviest element, Lithium (Li). Its ionization energy is 520 Kj/mol - oh, no! much lower than either hydrogen (1312 kJ/mol) or helium (2373 kH/mol). | 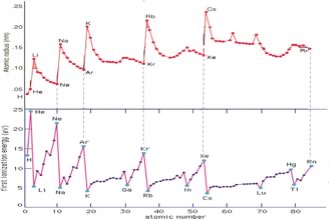 |
| So what do we conclude? First, it is clearly much easier (that is, requires less energy) to remove an electron from Li than from either H or He. This means that the most easily removed electron in Li is somehow different than are the most easily removed electrons of either H or He. Following our previous logic, we deduce that the electron must be further away (most of the time) from the nucleus - that is, we would predict that a Li atom will have a larger radius than either H or He atoms. So what do we predict for the next element, Beryllium (Be)? |
We might guess that it is smaller than Lithium and has a larger ionization energy because the electrons are attracted more strongly by the 4 positive charges in the nucleus. Again, this is the case, the ionization energy of Be is 899 kJ/mol, larger than Li, but much smaller than that of either hydrogen or helium. Following this trend, the atomic radius of Be is smaller than Li but larger than H or He. We could continue this way, empirically measuring ionization energies for each element, but how do we make sense of the patterns observed? |
2.1
Electrons & Orbitals |
Question to answer:
Questions to ponder:
|
| 27-Jun-2012 |