In science when we talk about a “rate” we mean the change in a quantity over time. As (non-chemical) examples, certain investments have an interest rate, which is the increase in the principle over time (if the rate were to be negative, then it was mean that the amount of principle would decrease over time, not a good investment!) Similarly, the rate at which you travel down the road (your speed) is given in miles per hour (or km/hr). A child might grow at the rate of an inch or two per year (while the aged can shrink), and some plants (like kudzu) can grow at the rate of a inches per day. The units of rate are (an amount) divided by (a period of time). While this might seem too obvious to dwell upon, it is worth noting that most real processes do not have a constant rate of change; rates themselves can, and do change – this is one reason why the calculus is useful in chemistry, since it provides the mathematical tools needed to deal with changing rates, like those associated with planetary motions, falling bodies, and (it turns out) chemical reactions.

8.1 How for, how fast?
8.2 Reaction rate
8.3 Activation energy
8.4 Catalysis
8.5 Equilibrium
8.6 Mechanisms

If we apply this same idea to the speed of a chemical reaction, what do we have to be able to measure to determine a reaction’s rate? What units tell us the amount of “stuff” present, in the same way that miles and meters measure distance? We can’t use mass, since reactions occur between particles (atoms, molecules, ions) which have different masses, so we have to use the unit that tells us how many particles of a particular type there are – that is, moles. Further, since most reactions (particularly the ones involved in biological and environmental) systems occur in aqueous solutions or in the atmosphere, we usually use units of concentration – that is: molarity (M, mol/L) to describe the amount of a substance taking part in, or produced by a reaction. Typically the concentration of substance A₂ is written [A₂], and the rate of a reaction can be described as the change in concentration (of a reactant or product) over a unit of time: that is, Δ[A2]/Δt or [A₂]₂ –[A₂]₁ / t₂ –t₁, where [A2]₂ is the concentration at time t₂, and [A2]₁ is the concentration at time t₁(assuming that t₂ occurs later in time than t₁).

Question to answer:

• What does linear mean (exactly) when referring to a graph?
• Imagine you are driving at a constant speed of 60 miles per hour. Draw a graph of distance versus time, over a time period of 4 hours.
• How would you determine your speed from the graph (assuming you did not already know the answer?)
• Now imagine you take your foot off the accelerator and the car coasts to a stop over the course of one hour. What is the average speed over the last hour? (How would you figure that out?).
• What is the speed exactly 30 minutes after you take your foot of the brake? (How would you figure that out?).
  

Reaction rates and probabilities

Let us now step back and think about what has to happen for a reaction to occur. First, the reactants will have to be mixed together. The best way to make a homogeneous mixture is to form solutions, and it is true that many reactions take place in solution. When reactions do involve a solid, like the rusting of iron, the reactants interact with one another at a surface. To increase the probability of such a reaction, it is common to use a solid that is very finely divided, so that it has a large surface area, allowing the reactants more places to collide.

We will begin a more in depth look at reaction rates with a simple hypothetical reaction that occurs slowly, but with a reasonable rate in solution. Our “toy” reaction will be A₂ + B₂ ↔ 2AB.  Since the reaction is slow, that means that the loss of reactants (A₂ + B₂) and the production of product (AB) will also be slow, but measurable.

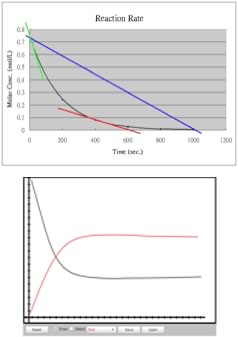Over a reasonable period of time, the concentrations of A₂, B₂ and AB change significantly. If we were to watch the rate of the forward reaction (A₂ + B₂ ↔ 2AB), we would find that it begins to slow down. One way to visualize this is if we plot the concentration of a reactant versus time, we see that the relationship between them is not linear, but falls off gradually as time increases. We can get measures of rates at any given time by taking the slope of the tangent to the line at that instant, and as you can see these slopes decrease as time goes by. On the other hand, immediately after mixing A₂ + B₂, we would find that the back reaction (that is 2AB ↔ A₂ + B₂) is zero – because of course there is no AB around to react, at least initially. As the forward reaction proceeds, however, the concentration of AB increases, and the back reaction rate increases (as indicated by the slopes of the tangents to the curve). Interestingly, as the reaction proceeds, the concentration of both the reactants and products reach a point where they do not change any further.

Question to answer:

• For the reaction A₂ + B₂ ↔ 2AB. If the rate of the forward reaction = – Δ[A₂]/Δt (at a given time). How would you write the rate in terms of [B₂] or in terms of [AB]?
• How does the rate of the forward reaction change over time?
• Does it increase, decrease or stay the same? Why?
  

Questions to ponder:

• Why do you think the amounts of products and reactants do not change after a certain time?
• What is the observable rate of reaction after the time when the concentrations of products and reactions change.

Let us now consider what is going on in molecular terms. For a reaction to occur (some of) the bonds holding the reactant molecules together must break, and new bond(s) must be formed to create the products. We can also think of forward and backward reactions in terms of probabilities. The forward reaction rate is determined by the probability that a collision between an A₂ and a B₂ molecule provides enough energy to break the A-A and B-B bonds, together with the probability of an AB molecule forming. The back reaction rate is determined by the probability that collisions (with surrounding molecules) will provide sufficient energy to break the A-B bond, together with the probability that the As and Bs released find other As and Bs to form A₂ and B₂ molecules. Remember, collisions are critical, since there are no “reactions at a distance”. What exact steps are involved in the forward and back reactions are not specified, but we can make a prediction - if these steps are unlikely to occur (low probability), the reactions will be slow.

As the reaction proceeds, the forward reaction rate will decrease because the concentrations of A₂ and B₂ decrease, while the back reaction rate will increase, as the concentration of AB increases. At some point, the two reaction rates will be equal and opposite - this is the point of equilibrium. This point could occur at a high concentration of AB or a low one, depending upon the reaction. At the macroscopic level we recognize the equilibrium state by the fact that there are no further changes in the concentrations of reactants and products, but this is due to the huge numbers of molecules involved.

It is important to understand that at the molecular level, the reactions have not stopped. For this reason we call the chemical equilibrium state - a dynamic equilibrium. We should also point out that the word equilibrium is misleading since in “everyday life” it is often used to mean a state of rest. In chemical systems, nothing could be further from the truth - even though there are no macroscopic changes observable, molecules are still reacting.

8.1 How for, how fast?
8.2 Reaction rate
8.3 Activation energy
8.4 Catalysis
8.5 Equilibrium
8.6 Mechanisms

Question to answer:

• What does a probability of “0” mean?
• How do we know that, at equilibrium,the forward and reverse reactions are still occurring?
• Design an experiment that would allow you to investigate whether a reaction had stopped: at the macroscopic level, at the molecular level
• What data would you have to collect to do this experiment at both levels (do not worry exactly about how to collect the data - just what to collect).
• Could you use the same data to answer both questions (that is, at the macroscopic and the molecular levels)?
  

Questions to ponder:

• Why can a macroscopic reaction be irreversible, even though the microscopic reaction is reversible?
• When would a reaction stop completely, under what (if any) conditions?
• Why are microscopic and macroscopic behaviors different?