Chapter 8.3: Activation energies and reaction kinetics

The study of reaction rates is called chemical kinetics, and encompasses a wide range of activities, measurements and calculations. You might wonder why anyone would bother with this, but it turns out that we can get more information about a reaction from kinetic data than just how fast it goes - more importantly we can get information about the pathway that the reaction takes from reactants to products - the mechanism of the reaction. If you think about a reaction in molecular terms, it seems clear that there must be a continuous pathway between reactants and products. The reactants do not suddenly disappear and then re-appear as products, and in most reactions only one or two bonds are broken and formed as the reaction proceeds. This pathway, what we call the mechanism, captures the order in which bonds are broken and formed, and the intermediate species involved.

 

8.1 How for, how fast?
8.2 Reaction rate
8.3 Activation energy
8.4 Catalysis
8.5 Equilibrium
8.6 Mechanisms
 

However, since we cannot directly see what happens (at the molecular level) during a reaction, we have to rely on indirect methods to determine what is going on. Even using modern spectroscopic techniques, some species in reaction pathways may only be present for femto (10–15) or atto (10–18) seconds. Events on these time scales are very difficult to study, and in fact much of the current cutting edge research in chemistry and physics is directed at detecting and characterizing such ephemeral molecular level events. As we will see,information about how the reaction rate varies with concentration and temperature can give us fascinating chemical insights into reaction pathways.

Concentrations and reaction rates

As the probability of collisions between reactant molecules increases, the rate of reaction increases. In order to get information about the reaction mechanism we need to know the exact relationship between concentrations and rates. This can be done using a number of different techniques and experimental set-ups. But before we look at that we need to go over a few more terms. Recall that the rate of the reaction is the change in concentration of reactant per unit time. If the time interval is measurable (that is, real) the rate we get is called the average rate (over that time interval). If we imagine that the time interval drops to 0, we can get the instantaneous rate - which is the slope of the tangent to the concentration versus time curve at a given time (more calculus). The rate at the beginning of the reaction can be obtained by taking the tangent at the start of the reaction (t=0). This instantaneous rate is useful in many situations because as the reactants form products, the product can interfere with or inhibit the forward reaction. This is particularly true in biological systems, where a product may inhibit its own formation, for example by binding to a site on the enzyme that catalyzes the reaction. This type of interaction is common, and often inhibits the enzyme’s activity (a form of feedback regulation).
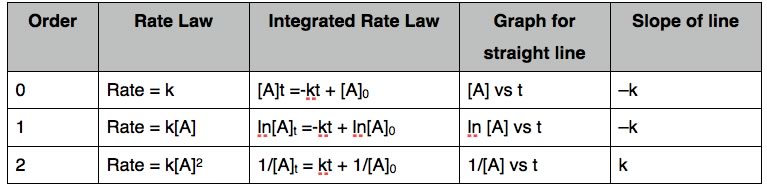
For example we could measure the initial rate for a reaction using different concentrations of reactants. Using an appropriate experimental design, we can figure out how the rate of the reaction varies with each reactant. For many common reactions, the relationship between the rate and the concentration is fairly straightforward.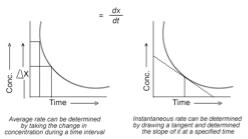

For example, in the reaction: (CH3)3CBr + –OH + Na+ ↔ (CH3)3COH + Br– + Na+|

the rate of this reaction is dependent only on the concentration of t-butyl bromide [(CH3)3CBr], not on the concentration of the sodium ion [Na+] or the hydroxide ion [–OH]. At this point you might be asking yourself - well why only the t-butyl bromide? We will get to that point shortly, because it gives us some very interesting and important insights into the reaction mechanism - but first - a bit more background.

Since the rate is directly proportional to the [(CH3)3CBr], we can write the relationship between rate and concentration as: rate ∝ [(CH3)3CBr], or we can put in a constant (k) to make the equation:
rate = k[(CH3)3CBr]. We could also write –Δ[(CH3)3CBr] /Δt = k[(CH3)3CBr], or if we let the time interval drop to zero –d[(CH3)3CBr] /dt = k[(CH3)3CBr]. In all these forms, the equation is known as the rate equation for the reaction. The rate equation must be experimentally determined. It is worth noting that you cannot write down the rate equation from considering the reaction equation (obviously in this case, since –OH or Na+ do not appear in the rate equation). The constant (k) is known as the rate constant, (and is completely different from the equilibrium constant (Keq)). The fact that they are both designated by k (one lower case and one upper case) is just one of those things we have to note and make sure not confuse which is which. A rate equation that only contains one concentration is called a first order rate equation, and the units of the rate constant are 1/time.

Now, in contrast to the first order reaction of methyl bromide and hydroxide, let us compare the reaction of methyl bromide with hydroxide.
CH3Br + –OH + Na+ ↔ CH3OH + Br– + Na+

For all intents and purposes these reactions appear to be exactly the same. That is, the bromine that was bonded to a carbon has been replaced by the oxygen of hydroxide. However, if we run the experiments, we find that the reaction rate depends on both the concentration of methyl bromide [CH3Br ] and on the hydroxide concentration [–OH]. The rate equation is: rate = k [CH3Br] [–OH]. How can this be? Why the difference? Well, the first thing it tells us is that something different is going on at the molecular level, the mechanisms of these reactions are different.

Reactions that depend on two concentrations are called second order reactions, and the units of k are different (you can figure out what they are by dimensional analysis).
In general:
rate = k [A] - first order
rate = k [A][B] - second order (first order in A and first order in B)
rate = k [A]2 second order (in A)
rate = k [A]2 [B] third order (second order in A and first order in B).

There are a number of methods for determining the rate equation for a reaction; here we will consider just two. One method is known as the “method of initial rates”. The initial rate of the reaction is determined, for various different starting concentrations of reactants. Clearly, the experimental design is of paramount importance here. Let us say you are investigating our reaction A + B → 2AB. The rate may depend on [A] and/or [B], therefore the initial concentrations of [A] and [B] must be carefully controlled. If [A] is changed in a reaction trial, then [B] must be held constant, and vice versa (you cannot change both concentrations at the same time since you would not know how each one affects the rate).

The method of initial rates means that you have to run the experiment multiple times. In contrast, the second method is known as the “graphical method”; it involves determining the rate equation, which involves only one run of the reaction. This method requires the collection of a set of concentration vs time data (the same data that you would collect to determine the rates). Ideally we would like to manipulate the data so that we can obtain a linear equation (y = mx +b). For example, if we have a set of [A] vs time data for a reaction, and we assume the reaction is first order in A, then we can write the rate equation as:  -d[A]/dt =k[A]

now if we separate the variables, [A] and t, to get:  -d[A]/[A] =kt

and then integrate the equation over the time period t= 0 to t =t to arrive at  ln [A]t = –kt + [A]0

As you will notice, this equation has the form of straight line; if we plot our data (ln [A] vs t ) and if the reaction is first order in [A], then we should get a straight line, where the slope of the line is –k. We can do a similar analysis for a reaction that might be second order in [A], that is rate - k[A]2, and in this case we can manipulate the rate equation and integrate to give the equation:1/[A]t = kt + 1/[A]0

Therefore, plotting 1/[A] vs t would give a straight line, with a slope of k, the rate constant. This method of analysis quickly becomes too complex for reactions with more than one reactant (that is reaction with rates that depend on both [A] and [B]), but you can look forward to that in your later studies!
table

Question to answer:

  • It turns out that most simple reactions are first or second order, can you think why?
  • Design an experiment to determine the rate equation for a reaction 2A + B → C. Using the method of initial rates, and a first experimental run using 0.1 M concentrations of all the reactants, outline the sets of initial conditions you would use to figure out what that rate equation is.
  • What is the minimum number of runs of the reaction that you would have to do? How would you determine the rate for each of your sets of conditions?
  • Now imagine you have determined that this reaction 2A + B --> C, does not depend on [B], outline a graphical method you could use to determine the rate equation. What data would you have to collect? What would you do with it?

Questions for later:

  • Why do you think we cannot just write the rate equation from the reaction equation?
  • Why do you think that the most common rate equations are second order?
Temperature and reaction rates

Temperature is another important factor in determining reaction rate. This makes sense if you remember that the vast majority of reactions involve collisions and that the effects of collisions are influenced by how fast the colliding objects are moving. We know intuitively that heating tends to make things happen. For example if you want something to cook faster you heat it to a higher temperature (and cooking, it turns out, is just a series of chemical reactions). Why should this be so? We have already seen that many reactions are exothermic, that is they give off energy, and raise the temperature. The reaction of hydrogen and oxygen, discussed in chapter 7, is an excellent example of this phenomenon. The reaction itself is highly exothermic – explosive in fact - yet a mixture of hydrogen and oxygen is quite stable unless energy is supplied, either by heating or a spark of electricity. The same is true of wood and molecular oxygen. The question is: what is the initial “spark” of energy being used for?

The answer lies with one of the principles that we have returned to over and over again: when atoms form bonds, the result is a more stable system (compared to the energy of unbonded atoms). But not all bonds are equally stable; some are more stable than others. Nevertheless, it always requires energy to disrupt a bond – any bond. If a reaction is to take place, then at least one of the bonds present in the reactants must be broken, a process that requires energy.

If we imagine two reactants approaching each other, as the reaction starts to occur, the first thing that happens is that the bond being broken must start to break. It is the initial partial bond breaking step(s) that requires an input of energy from the molecule’s surroundings, and the amount of energy required and available will determine if the reaction occurs. If the amount of energy in the environment is not enough to begin the breaking of bonds in the reactants (and, for example in the burning of wood large amounts of energy are required for the initial bond breaking), then the reaction will not occur without an energy “push”. Wood does not just burst into flames (at least at standard temperatures) - and neither do humans. The burning wood reaction (i.e. wood + O2 ↔ H2O + CO2) does not occur under normal conditions, but as the temperature rises enough, the reaction will start. Once the reaction starts, however, the energy released from the formation of new bonds is sufficient to raise the local temperature and so lead to the breaking of more bonds, the formation of new ones and the release of more energy. As long as there is wood and oxygen available, the system will behave as a positive and self-sustaining feedback look. The reaction will stop if one of the reactants becomes used up or the temperature is lowered. You might well ask yourself, “how is it that water extinguishes a fire?”
It is the “activation energy” associated with reactions that is responsible for the stability of our world. For example, we live in an atmosphere of ~20% O2. There are many molecules in our bodies and our environment that can react with O2. If there were no energy barriers to combustion (i.e. reaction with O2), we would burst into flames. Sadly, as Salem witches and others would attest (if they could), raise the temperature and we do burn. And, once we start burning, it is hard to stop the reaction. As we have said before, combustion reactions are exothermic, once they have produced enough thermal energy, the reaction d?oesn’t need that “spark” any more. But the requirement for that initial spark is why you need the addition of energy (such as provided by a detonator) for explosions to occur.

If we plot energy versus the progress of the reaction we can get a picture of the energy changes that go on during the reaction.

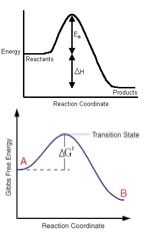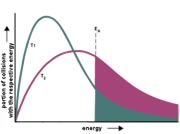
(Remember the reaction coordinate (x-axis) is not time since, as we have seen, reactions are going backwards and forwards all the time.) For a simple one-step reaction as shown here, the highest point on the energy profile is called the transition state. It is not a stable entity and only exists on the timescale of molecular vibrations (femtoseconds).

Now it is reasonably easy to understand how increasing temperature can increase the reaction rate - because it increases the average kinetic energy of the molecules in the environment. (As an aside, do you remember and understand that, even though individual molecules have different kinetic energies, all of the different populations of molecules in a system have the same average kinetic energy.) If we consider the effect of temperature on the distribution of kinetic energies (the Maxwell-Boltzman distribution), we see right away that at higher temperatures there are relatively more molecules with higher kinetic energy – it is collisions between these “high energy” molecules that provides the energy needed to overcome the activation energy barrier. This means that as the temperature rises, the probability of “productive” collisions occurring between particles per unit time increases, that is, the reaction rate will increase. At the same time, it is possible that raising the temperature will allow other reactions, perhaps reactions we have not been considering, to occur. This is particularly likely if we are dealing with complex mixtures of different types of molecules.

The rate equation does not appear to contain a term for temperature, and typically we have to specify the temperature at which the rate was measured. But since the rate changes with temperature, it must be the rate constant that changes. Sure enough, it has been determined experimentally that the rate constant k ∝ e–Ea/RT (or substituting a constant k = A e–Ea/RT), where k is the rate constant, Ea is the activation energy, T is the temperature, and R is a constant. This is known as the Arrhenius equation, and you can see by inspection that k is directly proportional to the temperature, and indirectly proportional to the activation energy Ea (can you see that?)


The constant A is sometimes called the frequency factor - and has to do with the collision rate; it depends on the specific type of reaction (unlike R, the gas constant, which does not change from reaction to reaction). One way of thinking about the rate constant is to consider it as a representation of the probability that a collision will lead to products - the larger the rate constant, the more frequently productive collisions occur and the faster the reaction.

The activation energy for a reaction also depends upon the type of reaction that is occurring. For example, a Brønsted-Lowry acid base reaction has a very low activation energy barrier. In these reactions the only thing that is happening is that a proton is being transferred from one electronegative element to another.
H–Cl + H–O–H ? Cl– + H3O+ (draw out)

The reaction is rapid because the Cl-H bond is highly polarized, it is weak; in a sense it is already partially broken, especially since these reactions usually take place in water - which interacts with and stabilizes the growing charges. Low energy collisions with water molecules are sufficient to finish breaking the Cl-H bond. We say that acid-base reactions like this are kinetically controlled, they occur on mixing and do not require heating up or extra energy to make them go because essentially all collisions involving the HCl molecule provide sufficient energy to break the H-Cl bond. This is also true for almost all proton transfer reactions. However, for most other types of reactions, simply mixing the reactants is not enough, and either energy has to be supplied to the system to overcome this energy barrier, or we have to wait a long time for the reaction to occur. In fact, most organic reactions (that is reactions in which carbon is involved) are quite slow. Why the difference? (the answer should be reasonably obvious.) There is simply not enough energy in the vast majority of the collisions between molecules to break a C-H, C-C, C-N, or C-O bond. If you take organic chemistry lab, you will discover that large portions of the time are spent waiting as solutions are heated to make reactions happen faster.

 

As we mentioned before, this is quite fortunate, since we are (basically) organized by chance and natural selection, from collections of organic reactions. If these reactions occurred spontaneously and rapidly, we would fall apart and approach equilibrium (and equilibrium for living things means death!) But you may have identified a potential problem, generally it is not advisable to heat up a biological system, and we certainly do need biological systems to undergo reactions. We would like different reactions to proceed in different places and at different rates. For this, biological systems (and many others) use a wide range of catalysts.

 

8.1 How for, how fast?
8.2 Reaction rate
8.3 Activation energy
8.4 Catalysis
8.5 Equilibrium
8.6 Mechanisms

Question to answer:

  • When a reaction releases energy, where does the energy come from?
  • There is a rule of thumb that increasing the temperature by 10°C will double the rate for many reactions.
  • What factor in the Arrhenius equation must be changing?
  • Explain why the reaction rate increases when the temperature increases.
28-Jun-2012